Segré-Silberberg effect¶
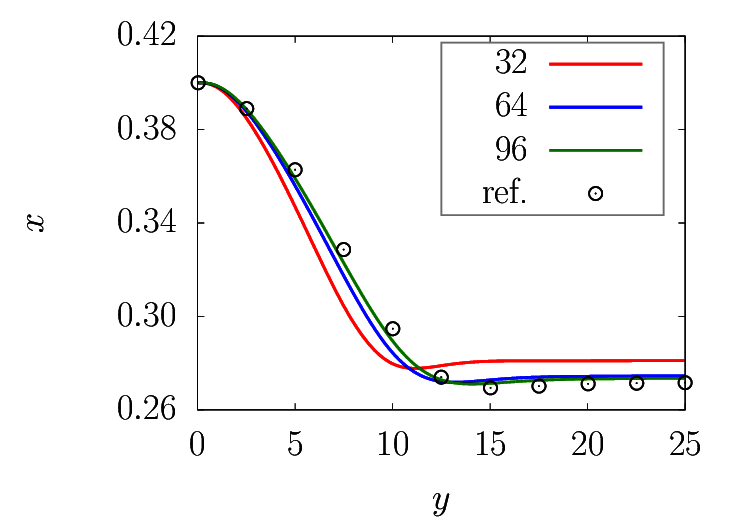
Comparison with the reference data by Pan and Glowinski, J. Comput. Phys. (181), 2002 is described, who simulated the Segré-Silberberg effect in a two-dimensional wall-bounded domain by means of the fictitious domain method.
Configuration¶
We consider a square domain (\(l_x = l_y = 1\)), in which a circular object (whose radius is \(0.125\)) is positioned at \(x = 0.4, y = 0\). Everything is stationary at \(t = 0\), and the liquid (viscosity is adjusted so that the bulk Reynolds number leads \(2334\)) and particle start to move because of a constant forcing in \(y\) (stream-wise) direction, whose magnitude is \(-dp / dy = 2.337 \times 10^{-4}\). Spatial resolutions are varied from \(32\) to \(96\) grids per domain size (\(8\) to \(24\) grids per diameter) to check the spatial convergence.
In practice, the configuration is specified as follows (\(32\) grids per domain):
#!/bin/bash
## directory name containing flow fields to restart
# export dirname_restart="output/save/stepxxxxxxxxxx"
## durations
# maximum duration (in free-fall time)
export timemax=7.5e+2
# maximum duration (in wall time [s])
export wtimemax=6.0e+2
# logging rate (in free-fall time)
export log_rate=1.0e+0
# logging after (in free-fall time)
export log_after=0.0e+0
# save rate (in free-fall time)
export save_rate=1.0e+3
# save after (in free-fall time)
export save_after=0.0e+0
# statistics collection rate (in free-fall time)
export stat_rate=1.0e-1
# statistics collection after (in free-fall time)
export stat_after=2.0e+3
## domain
# domain lengths
export ly=1.0e+0
# number of grids
export itot=32
export jtot=32
## dt safe factors, adv and dif
export safefactor_adv=0.75
export safefactor_dif=0.75
## physical parameters
export Re=2.334e+3
# export Fr=1.e+0
## external forcing in y direction
export extfrcy=2.337e-4
mpirun -n 1 --oversubscribe ./a.out
Results¶
Note
Conducted by GitHub Actions.
OS : "Ubuntu 22.04.3 LTS"
Date : Sat Feb 10 13:46:41 UTC 2024
Hash : bc64913d53d88051808a651acdffa80b0fbaada0
OS : "Ubuntu 22.04.3 LTS"
Date : Sat Feb 10 13:47:12 UTC 2024
Hash : bc64913d53d88051808a651acdffa80b0fbaada0
OS : "Ubuntu 22.04.3 LTS"
Date : Sat Feb 10 13:47:49 UTC 2024
Hash : bc64913d53d88051808a651acdffa80b0fbaada0
The final flow field is shown below. Note that the picture is transposed, i.e., in the picture, \(x\) and \(y\) directions in the simulation are shown as the vertical and horizontal directions, respectively.
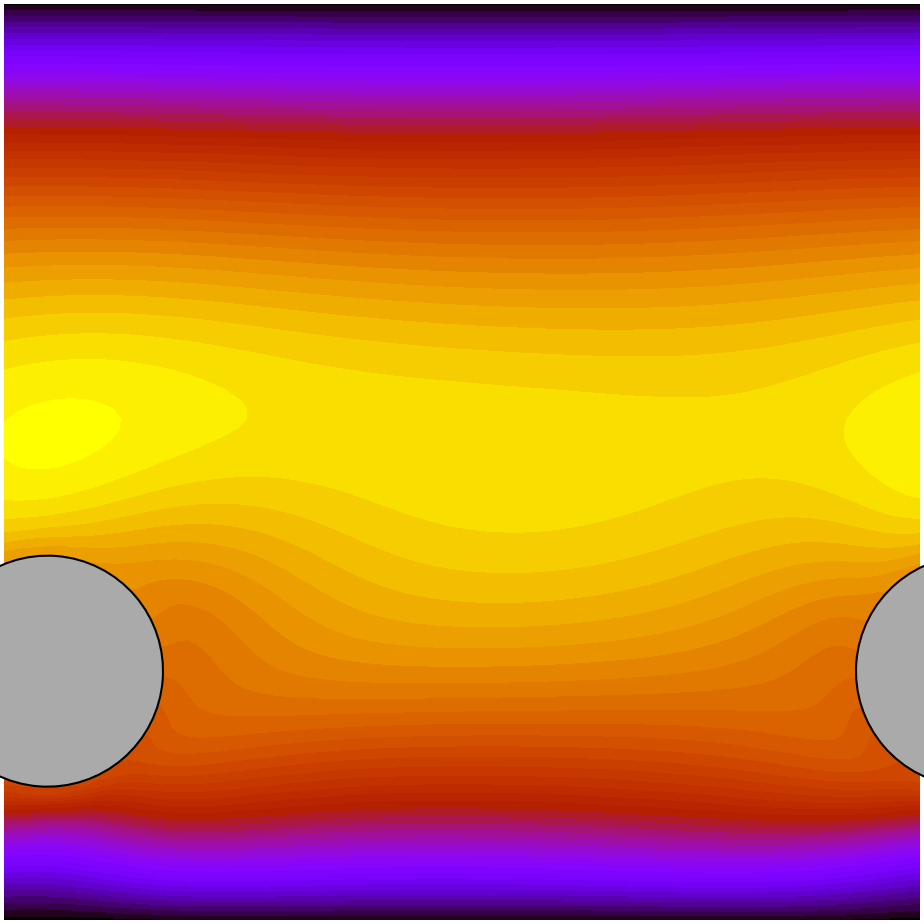
The colour denotes the size of the stream-wise velocity, while the center gray object is the immersed particle.
Lateral (wall-normal, \(x\) direction) migration of a particle as a function of the traveling distance in the stream-wise (\(y\)) direction is shown below.