Collision of Ellipses¶

In this part I consider the collisions between two ellipses; namely, in this picture:

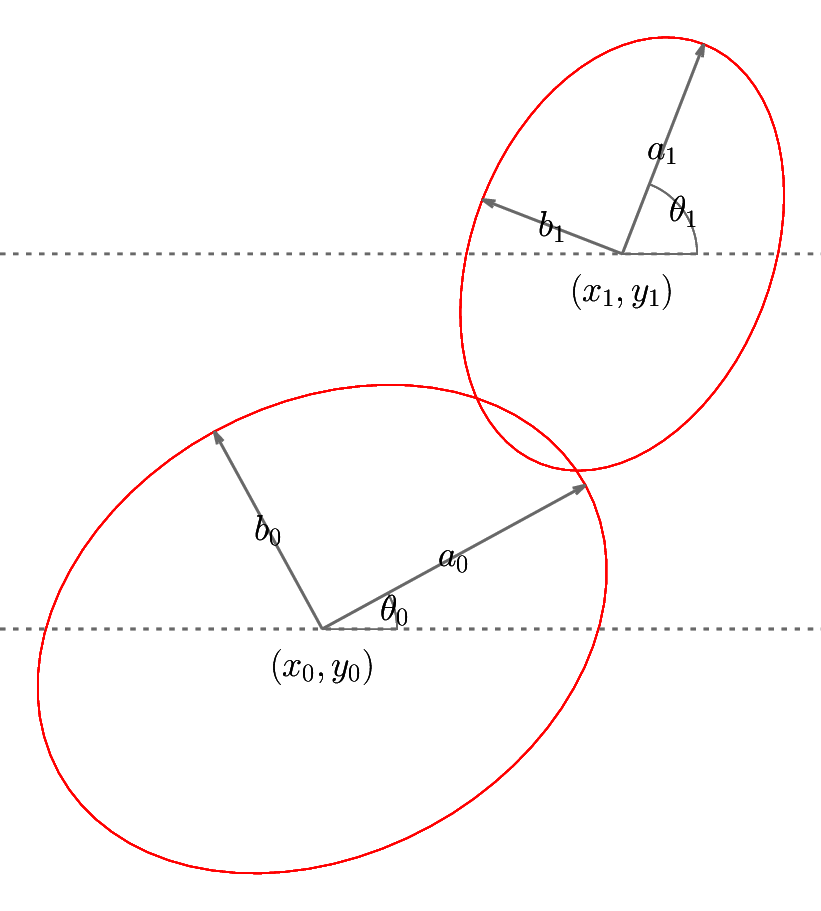
I aim at investigating

whether the two ellipses collide,
if they do, how much the penetration depth \(\delta\) is.

I assume the ellipses are completely smooth and rigid (i.e. no deformation), and \(\delta\) is sufficiently small compared to the size of the ellipses.

Note

This is a rough solution to obtain something plausible just to avoid the over-penetration between objects. Neither the collision detection nor the quantification of \(\delta\) are rigorous.

Problem setup¶

An ellipse whose center is at the origin and the major / minor axes are \(a_0\) and \(b_0\) is given by

\[\frac{x_e^2}{a_0^2} + \frac{y_e^2}{b_0^2} = 1.\]

By introducing a parameter \(t_0\), this equation reads

\[\begin{split}\begin{pmatrix} x_e \\ y_e \end{pmatrix} = \begin{pmatrix} a_0 \cos t_0 \\ b_0 \sin t_0 \end{pmatrix}.\end{split}\]

To take into account the rotation of \(\theta_0\) and off-centred objects whose centre is at \(\left( x_0, y_0 \right)\), I modify the equation as

\[\begin{split}\begin{pmatrix} x_e \\ y_e \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + \begin{pmatrix} \cos \theta_0 & -\sin \theta_0 \\ \sin \theta_0 & \cos \theta_0 \end{pmatrix} \begin{pmatrix} a_0 \cos t_0 \\ b_0 \sin t_0 \end{pmatrix}.\end{split}\]

Hereafter subscripts \(0,1\) are used to distinguish the two ellipses.

The collision / intersection of the two ellipses results in a quartic equation with respect to the intersecting point(s) \(x\) (or \(y\)). The solution can be categorised as follows:

Four real solutions

Four intersecting points
Two real and two imaginary solutions

Two intersecting points
Four imaginary solutions

No Collision
And more

We are interested in distinguishing the second and the third cases. Note that the other cases are out of focus, since we assume that the collision depth is small enough.

Although we know a quartic formula, it is non-trivial to treat it numerically. Also, let’s say we obtain a theoretical solution; it is, however, still unclear how we define the penetration depth \(\delta\).

For these reasons, instead of solving quartic equations, I consider a simpler and approximated solution in this project.

Collision check using circular fitting¶

Although ellipses can rotate and be off-centered, by transforming the coordinate system:

\[\begin{split}\begin{pmatrix} x_p \\ y_p \end{pmatrix} \leftarrow \begin{pmatrix} \cos ( -\theta) & - \sin ( -\theta) \\ \sin ( -\theta) & \cos ( -\theta) \end{pmatrix} \begin{pmatrix} x_p-x_0 \\ y_p-y_0 \end{pmatrix},\end{split}\]

we are able to say one object is at the origin and does not rotate (the major axis coincides with the Cartesian \(x\) axis).

Circular approximation¶

Note

This part is largely inspired by Simple Method for Distance to Ellipse.

Recall that I consider situations where \(\delta\) is much smaller than the sizes of the colliding objects. This allows me to think that collisions between two circles fitting the ellipses in the vicinity of the colliding points well approximates the collisions between ellipses.

Collisions between two circles are much simpler; the penetration depth of two circles (not a rigorous definition but one sound candidate) leads to

\[\delta \equiv r_0 + r_1 - d,\]

where \(r_0\) and \(r_1\) are radii of the two circles, and \(d\) is center-to-center distance.

Now the main focus is how to approximate an ellipse using a circle in a systematic way. Actually there is an analytical circle which approximates an ellipse locally:

\[\left( x_c, y_c \right) = \left( a \left( 1 - \frac{b^2}{a^2} \right) \cos^3 t, b \left( 1 - \frac{a^2}{b^2} \right) \sin^3 t \right),\]

which is known as evolute. The local curvature is given by

\[\kappa = \frac{ ab }{ \sqrt{\left( a^2 \sin^2 t + b^2 \cos^2 t \right)^3} },\]

whose reciprocal is the radius of the circle fitting the original ellipse.

The only unknown is \(t\) which gives a circle nicely approximating the ellipse locally.

Finding a nice \(t\) is equal to find a normal vector from the point \(( x_p, y_p )\) to the ellipse, and also is equal to find the minimum distance to the ellipse.

Although these lemmas are not proved here, the following picture gives a good indication:

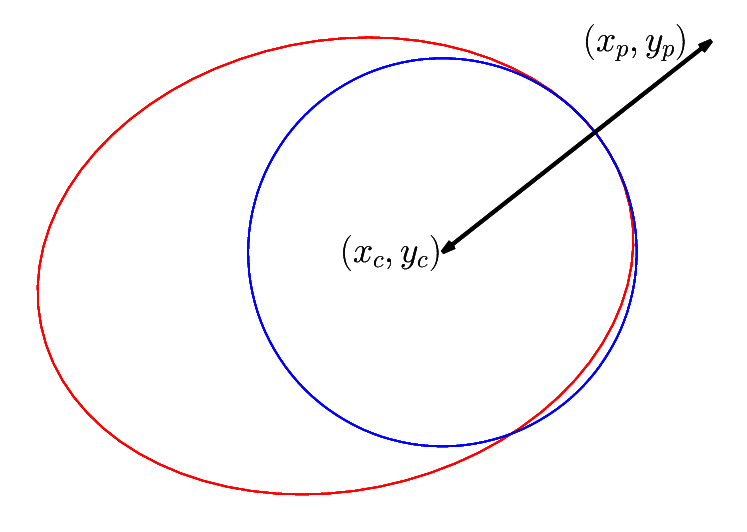
Here,

the black arrow connecting \(( x_p, y_p )\) and \(( x_c, y_c )\) gives a normal vector to the ellipse,
the fitted circle gives a good approximation of the ellipse locally.

Collision of two ellipses¶

I use the above method to quantify the penetration depth \(\delta\), which is very simple: for the ellipse \(i\), the center of the fitted circle of the ellipse \(j\) \(( x_{c_j}, y_{c_j} )\) is used as the target point \(( x_{p_i}, y_{p_i} )\) to fit a circle. This process is iterated until the locations of \(( x_{c_i}, y_{c_i} )\) converge.

When the two ellipses are colliding, the fitting circles lead

When the two ellipses are not colliding, the final state leads

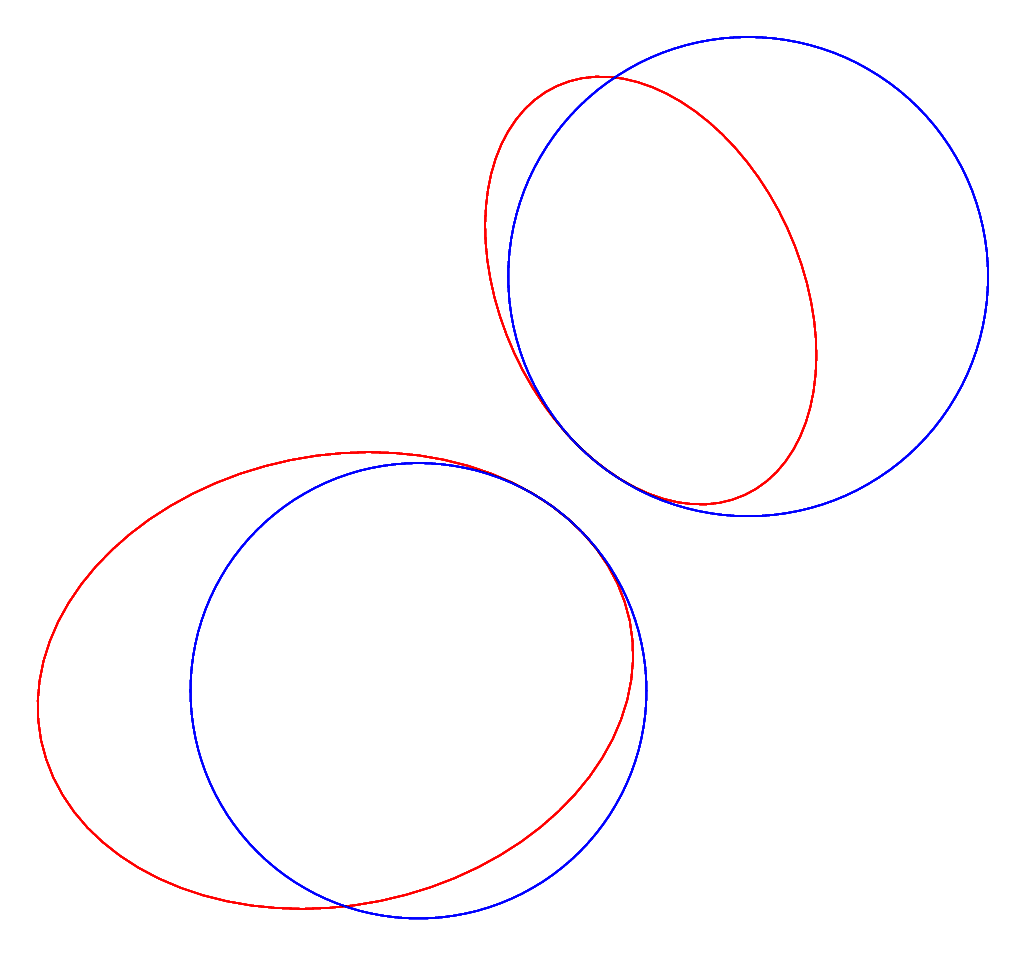
Since we now know nice circles, the penetration depth is simply

\[\delta \equiv r_0 + r_1 - d,\]

where, again, \(r_i\) are radii of the fitted circles, while \(d\) is the distance between the two centers of the fitting circles. Obviously two circles collide when \(\delta > 0\) and do not otherwise.

Stand-alone implementation¶

import numpy as np
from matplotlib import pyplot
from matplotlib import patches


def shift_and_rotate(disp, angle, p0):
    # shift a point p0, then rotate it
    # return the resulting point p1
    p1 = dict()
    x = p0["x"]+disp["x"]
    y = p0["y"]+disp["y"]
    p1["x"] = np.cos(angle)*x - np.sin(angle)*y
    p1["y"] = np.sin(angle)*x + np.cos(angle)*y
    return p1


def rotate_and_shift(disp, angle, p0):
    # rotate a point (x0, y0), then shift it
    # return the resulting point p1
    p1 = dict()
    x = p0["x"]
    y = p0["y"]
    p1["x"] = disp["x"] + np.cos(angle)*x - np.sin(angle)*y
    p1["y"] = disp["y"] + np.sin(angle)*x + np.cos(angle)*y
    return p1


def compute_evolute(e, t):
    # compute center of evolute and radius of fitted circle
    evolute = dict()
    a = e["a"]
    b = e["b"]
    evolute["x"] = a*(1.-np.power(b/a, 2.))*np.power(np.cos(t), 3.)
    evolute["y"] = b*(1.-np.power(a/b, 2.))*np.power(np.sin(t), 3.)
    num = np.power(np.power(a*np.sin(t), 2.)+np.power(b*np.cos(t), 2.), 1.5)
    den = a*b
    evolute["r"] = num/den
    return evolute


def find_normal_t(e, p):
    # compute parameter t, with which a point (a*cos(t), b*sin(t))
    # and the target point p gives a normal vector to the given ellipse
    # ref: https://blog.chatfield.io/simple-method-for-distance-to-ellipse/
    t = 0.25*np.pi
    while True:
        xe = e["a"]*np.cos(t)
        ye = e["b"]*np.sin(t)
        evolute = compute_evolute(e, t)
        dxe = xe-evolute["x"]
        dye = ye-evolute["y"]
        dxp = abs(p["x"])-evolute["x"]
        dyp = abs(p["y"])-evolute["y"]
        norme = np.hypot(dxe, dye)
        normp = np.hypot(dxp, dyp)
        dc = norme*np.arcsin((dxe*dyp-dye*dxp)/(norme*normp))
        dt = dc/np.sqrt(e["a"]**2.+e["b"]**2.-xe**2.-ye**2.)
        t += dt
        # limit in the first quadrant
        t = min(t, 0.5*np.pi)
        t = max(t,        0.)
        if abs(dt) < 1.e-8:
            break
    # apply result to the other quadrants
    if p["x"] < 0.:
        t = -t+np.pi
    if p["y"] < 0.:
        t = -t
    return t


def fit_circles(e0, e1):
    # core function, fitting two circles
    # read the documentation
    for n in range(10):
        if n == 0:
            # initialise temporary evolute
            p0 = {"x": e0["x"], "y": e0["y"]}
            p1 = {"x": e1["x"], "y": e1["y"]}
        # forward coordinate transform
        disp = {"x": -e0["x"], "y": -e0["y"]}
        angle = -e0["theta"]
        p1_ = shift_and_rotate(disp, angle, p1)
        # forward coordinate transform
        disp = {"x": -e1["x"], "y": -e1["y"]}
        angle = -e1["theta"]
        p0_ = shift_and_rotate(disp, angle, p0)
        # find optimum parameter t for each ellipse
        e0_t = find_normal_t(e0, p1_)
        e1_t = find_normal_t(e1, p0_)
        # compute evolutes and their radii
        evolute0_ = compute_evolute(e0, e0_t)
        evolute1_ = compute_evolute(e1, e1_t)
        # backward coordinate transform
        disp = {"x": +e0["x"], "y": +e0["y"]}
        angle = +e0["theta"]
        p0 = rotate_and_shift(disp, angle, evolute0_)
        # backward coordinate transform
        disp = {"x": +e1["x"], "y": +e1["y"]}
        angle = +e1["theta"]
        p1 = rotate_and_shift(disp, angle, evolute1_)
    evolute0 = {"x": p0["x"], "y": p0["y"], "r": evolute0_["r"]}
    evolute1 = {"x": p1["x"], "y": p1["y"], "r": evolute1_["r"]}
    return evolute0, evolute1


def plot_result(e0, e1, c0, c1):
    # wrapper of matplotlib.patches to visualise
    # resulting ellipses and fitted circles
    def get_patch_of_ellipse(e):
        x = e["x"]
        y = e["y"]
        width = 2.*e["a"]
        height = 2.*e["b"]
        angle = 180./np.pi*e["theta"]
        keywords = {
                "xy": (x, y),
                "width": width,
                "height": height,
                "angle": angle,
                "fc": "none",
                "ec": "#FF0000",
        }
        return patches.Ellipse(**keywords)

    def get_patch_of_circle(c):
        x = c["x"]
        y = c["y"]
        radius = c["r"]
        keywords = {
                "xy": (x, y),
                "radius": radius,
                "fc": "none",
                "ec": "#0000FF",
        }
        return patches.Circle(**keywords)

    def compute_bounds(es, cs):
        # determine plot ranges
        # i.e., arguments of set_[xy]lim
        xmin = +np.inf
        xmax = -np.inf
        ymin = +np.inf
        ymax = -np.inf
        for e in es:
            xmin = min(xmin, e["x"]-max(e["a"], e["b"]))
            xmax = max(xmax, e["x"]+max(e["a"], e["b"]))
            ymin = min(ymin, e["y"]-max(e["a"], e["b"]))
            ymax = max(ymax, e["y"]+max(e["a"], e["b"]))
        for c in cs:
            xmin = min(xmin, c["x"]-c["r"])
            xmax = max(xmax, c["x"]+c["r"])
            ymin = min(ymin, c["y"]-c["r"])
            ymax = max(ymax, c["y"]+c["r"])
        margin = 0.25
        xmin -= margin
        xmax += margin
        ymin -= margin
        ymax += margin
        return (xmin, xmax), (ymin, ymax)
    # prepare matplotlib objects
    fig = pyplot.figure()
    ax = fig.add_subplot(111)
    # draw ellipses and circles
    ax.add_patch(get_patch_of_ellipse(e0))
    ax.add_patch(get_patch_of_ellipse(e1))
    ax.add_patch(get_patch_of_circle(c0))
    ax.add_patch(get_patch_of_circle(c1))
    # set auxiliary parameters
    xlim, ylim = compute_bounds([e0, e1], [c0, c1])
    keywords = {
            "xlim": xlim,
            "ylim": ylim,
            "aspect": "equal",
    }
    ax.set(**keywords)
    # visualise
    pyplot.show()
    # clean-up
    pyplot.close()


if __name__ == "__main__":
    # initialise ellipses
    e0 = {"a": 2.0, "b": 1.5, "x": 0.5, "y": 0.5, "theta": 0.2}
    e1 = {"a": 1.5, "b": 1.0, "x": 2.0, "y": 2.5, "theta": 2.0}
    # fit circles
    c0, c1 = fit_circles(e0, e1)
    # plot
    plot_result(e0, e1, c0, c1)

Collision of Ellipses¶

Problem setup¶

Collision check using circular fitting¶

Circular approximation¶

Collision of two ellipses¶

Stand-alone implementation¶

Ellises in Flows

Navigation

Related Topics