Numerical method

Immersed boundary method

As being discussed in the governing equations, the fluid-structure interactions (momentum exchange) is taken care of by a forcing term \(a_i\). There are several ways to formulate \(a_i\), and one of the most successful ways is the direct forcing on Lagrange points defined on each particle surface (Uhlmann, J. Comput. Phys. (209), 2005). Here, on the other hand, we exchange the momentum between particles and fluid directly on the Eulerian field (e.g., Kajishima and Takiguchi, Int. J. of Heat Fluid Flow (23-5), 2002):

\[a_i \equiv w \frac{ U_i + \epsilon_{ijk} \Omega_j r_k - u_i }{\Delta t},\]

so that the no-slip / no-penetration conditions are imposed on the particle surface, where \(w\) is an appropriate weight. In this project, we adopt

\[f^{\prime} \left( x \right) = \frac{1}{2} \beta \left\{ 1 - \tanh^2 \left( \beta x \right) \right\}\]

as an approximation of Dirac delta, where \(x\) is the signed distance (\(x > 0\) and \(x < 0\) for inside and outside particles) from the particle surface normalised by the reference grid size \(\Delta \equiv \Delta x \equiv \Delta y\). One of the indefinite integrals of \(f^{\prime} \left( x \right)\) is

\[f \left( x \right) = \frac{1}{2} \left\{ 1 + \tanh \left( \beta x \right) \right\},\]

which is used in the THINC method (one type of the volume-of-fluid methods, see e.g., Xiao et al., Int. J. Numer. Method Fluid (48-9), 2005) as an phase indicator.

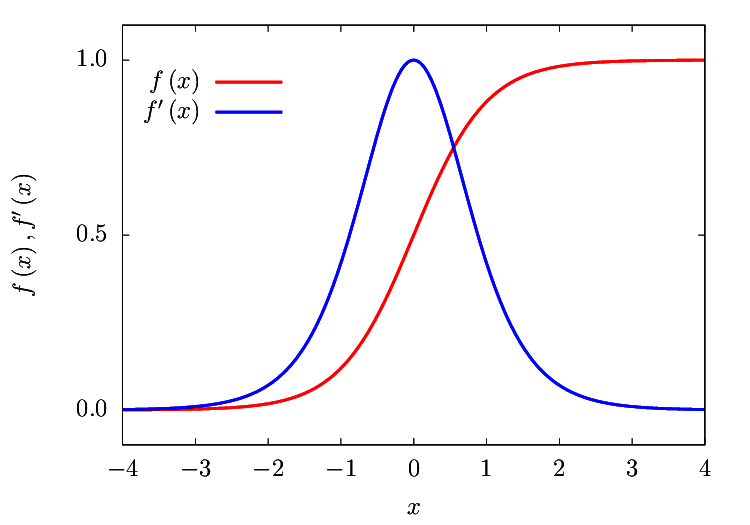
\(\beta\) controls the sharpness of the surface, and the larger \(\beta\) is, the sharper the surface is. \(\beta \rightarrow \infty\) in theory for rigid objects. For the time being, \(\beta\) is fixed to \(2\) so that \(f^{\prime} \left( d = 0 \right) = 1\), whose effects should be further investigated.

Temporal integration

Basically we adopt the three-step Runge-Kutta method to integrate all equations. The evolution of momentum from a Runge-Kutta step \(k\) to \(k+1\) is given as

\[\frac{ u_i^{k+1} - u_i^{k } }{\Delta t} = \left( rhs \right)_i^{k} + a_i^{k+\frac{1}{2}},\]

where \(\left( rhs \right)_i\) includes all single-phase contributions:

\[\left( rhs \right)_i^{k} \equiv - \gamma^k \dder{p}{x_i}^{k} + \alpha^k \left( adv + dif \right)_i^{k } + \beta^k \left( adv + dif \right)_i^{k-1}.\]

Note that the diffusive terms are treated explicitly in time for simplicity.

\(a_i\) is the response from the immersed object, which is defined as

\[a_i^{k+\frac{1}{2}} \equiv \frac{ u_i^{bnd} - u_i^{k } }{\Delta t} - \left( rhs \right)_i,\]

so that the fluid velocity at \(k+1\) step \(u_i^k\) is equal to the velocity of the boundary \(u_i^{bnd}\). We can simplify the right-hand-side by employing the prediction velocity \(u_i^*\), which is

\[u_i^{* } = u_i^{k } + \Delta t \left( rhs \right)_i^{k}\]

and thus the forcing leads

\[a_i^{k+\frac{1}{2}} \equiv \frac{ u_i^{bnd} - u_i^{* } }{\Delta t}.\]

See Uhlmann, J. Comput. Phys. (209), 2005 for details.

Note that the last updated velocity does not satisfy the continuity condition, which should be corrected by solving a pressure Poisson equation.

The whole procedure is as follows.

1. Predict

   \[\frac{ u_i^{* } - u_i^{k } }{\Delta t} = \left( rhs \right)_i^{k },\]

   which is taken care of by fluid_update_velocity.

2. Compute forcing

   \[a_i^{k+\frac{1}{2}} \equiv \frac{ u_i^{bnd} - u_i^{* } }{\Delta t},\]

   which is taken care of by suspensions_exchange_momentum.

3. Update velocity

   \[\frac{ u_i^{**} - u_i^{* } }{\Delta t} = a_i^{k+\frac{1}{2}},\]

   which is taken care of by suspensions_update_momentum_fleid.

4. Enforce continuity

   The last velocity \(u_i^{**}\) does not satisfy the continuity condition in general and thus we need to enforce it by solving a Poisson equation, which is identical to the single-phase counterpart.

5. Update particles

   Once the fluid variables are updated, particle velocities and positions are updated. In order to stabilise, we update them with a semi-implicit method (Crank-Nicolson scheme) iteratively.

   In particular, we solve

   \[\delta U_i \equiv U_i^{k+1} - U_i^{k } = - \frac{\gamma \Delta t}{m_p} \int a_i dS + \frac{1}{m_p} \int u_i dV + \frac{\gamma \Delta t}{2} \left( F_i^{k+1} + F_i^{k } \right)\]

   and

   \[\delta X_i \equiv X_i^{k+1} - X_i^{k } = \frac{\gamma \Delta t}{2} \left( U_i^{k+1} + U_i^{k } \right)\]

   iteratively until the particle locations converge (notice that \(F_i^{k+1}\) is a function of \(X_i^{k+1}\)). In practice, four iterations are sufficient to get converged, whose maximum number is substepmax in src/main.c.

   The computations of the right-hand-sides are taken care of by suspensions_increment_particles, while the update process (left-hand-sides) are done by suspensions_update_particles, respectively. For very high volume fraction (e.g., \(\varphi > 40\%\)), larger number might be needed to have a stable solution.