Numerical flux

In the previous step, I have obtained the surface function

\[\psi \left( X, Y \right) + d \equiv n_X X + n_Y Y + d,\]

and its diffused representation

\[\hat{H} \left( X, Y \right) \equiv \frac{1}{ 1 + \exp{ \left\{ -2 \beta \left( \psi + d \right) \right\} } }\]

for each cell center \(\left( \pic, \pjc \right)\).

In this section, I compute the numerical flux

\[\frac{1}{V_{ij}} \int_{\partial V} u_j \hat{H} n_j dS\]

to integrate the avection equation and to update \(\phi\).

Explicitly, on a two-dimensional Cartesian domain, this integral is consisted of four terms:

\[\int_{x, \pim} \ux \hat{H} dy - \int_{x, \pip} \ux \hat{H} dy + \int_{y, \pjm} \uy \hat{H} dx - \int_{y, \pjp} \uy \hat{H} dx\]

divided by the cell size

\[V_{ij} = \Delta x_{\pic} \Delta y.\]

Now I focus the first term, and the other terms can be evaluated in the same manner.

First of all, since \(\ux\) is constant on the local cell face, I can take it out of the integral:

\[\frac{1}{\Delta x_i \Delta y} \ux \int_{x, \pim} \hat{H} dy.\]

To stabilise the cell-face integral, I need to use the upward scheme: namely information of the upwind cell should be used, i.e.

\[\begin{split}\vat{\hat{H}}{\pimm, \pjc} \,\, & \text{if} \,\, \vat{\ux}{\pim, \pjc} \ge 0, \\ \vat{\hat{H}}{\pic, \pjc} \,\, & \text{if} \,\, \vat{\ux}{\pim, \pjc} < 0.\end{split}\]

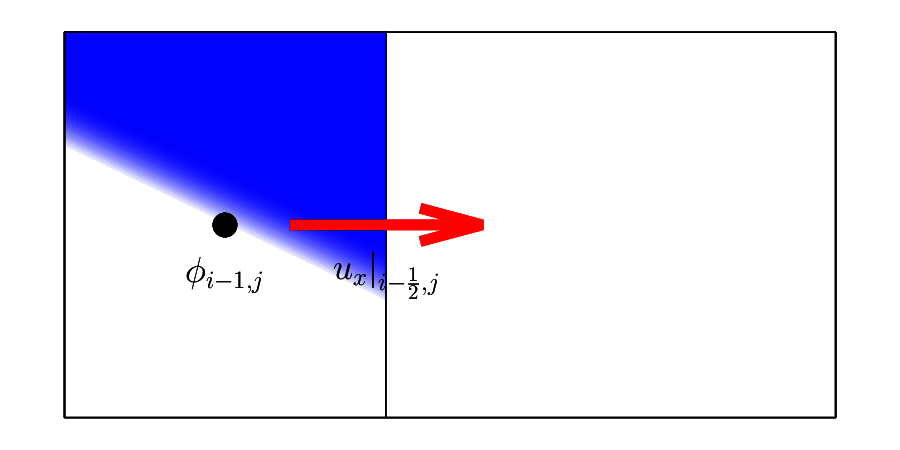
\(\vat{\ux}{\pim, \pjc} \ge 0\)

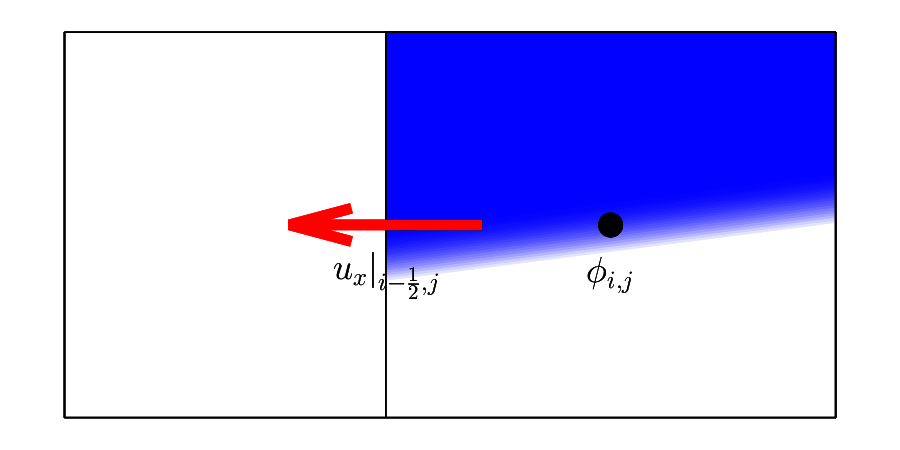
\(\vat{\ux}{\pim, \pjc} < 0\)

Recall that \(\hat{H}\) is defined on the local coordinate system attached to each cell center. Thus, for the left cell \(\left( \pimm, \pjc \right)\), the integrand should be evaluated at \(x = \frac{1}{2}\), while \(x = -\frac{1}{2}\) for the right cell \(\left( \pic, \pjc \right)\).

Same applied to the all fluxes.

src/interface/update/flxx.c

const double vel = UX(i, j);
const int    ii = vel < 0. ?    i : i - 1;
const double  x = vel < 0. ? -0.5 :  +0.5;

src/interface/update/flxx.c

const double vel = UX(i, j, k);
const int    ii = vel < 0. ?    i : i - 1;
const double  x = vel < 0. ? -0.5 :  +0.5;

src/interface/update/flxy.c

const double vel = UY(i, j);
const int    jj = vel < 0. ?    j : j - 1;
const double  y = vel < 0. ? -0.5 :  +0.5;

src/interface/update/flxy.c

const double vel = UY(i, j, k);
const int    jj = vel < 0. ?    j : j - 1;
const double  y = vel < 0. ? -0.5 :  +0.5;

src/interface/update/flxz.c

const double vel = UZ(i, j, k);
const int    kk = vel < 0. ?    k : k - 1;
const double  z = vel < 0. ? -0.5 :  +0.5;

Also notice that

\[dy = \der{y}{Y} dY \approx \Delta y dY,\]

and thus

\[\begin{split}\frac{1}{\Delta x_i \Delta y} \ux \int_{x, \pim} \hat{H} dy = \begin{cases} \ux \ge 0 & \frac{1}{\Delta x_i} \ux \int_{x = +\frac{1}{2}} \hat{H} dY_{i-1, j}, \\ \ux < 0 & \frac{1}{\Delta x_i} \ux \int_{x = -\frac{1}{2}} \hat{H} dY_{i , j}, \end{cases}\end{split}\]

whose integral is again approximated by the \(N\)-th-order Gaussian quadrature:

\[\frac{1}{\Delta x_i} \ux \sum_{j}^N w_j \hat{H} \left( x, y_j \right),\]

which is implemented here:

src/interface/update/flxx.c

const double lvof = VOF(ii, j);
if(lvof < vofmin || 1. - vofmin < lvof){
  FLXX(i, j) = vel * lvof;
  continue;
}
double flux = 0.;
for(int jj = 0; jj < NGAUSS; jj++){
  const double w = gauss_ws[jj];
  const double y = gauss_ps[jj];
  flux += w * indicator(NORMAL(ii, j), (const double [NDIMS]){x, y});
}
FLXX(i, j) = vel * flux;

src/interface/update/flxx.c

const double lvof = VOF(ii, j, k);
if(lvof < vofmin || 1. - vofmin < lvof){
  FLXX(i, j, k) = vel * lvof;
  continue;
}
double flux = 0.;
for(int kk = 0; kk < NGAUSS; kk++){
  for(int jj = 0; jj < NGAUSS; jj++){
    const double w = gauss_ws[jj] * gauss_ws[kk];
    const double y = gauss_ps[jj];
    const double z = gauss_ps[kk];
    flux += w * indicator(NORMAL(ii, j, k), (const double [NDIMS]){x, y, z});
  }
}
FLXX(i, j, k) = vel * flux;

src/interface/update/flxy.c

const double lvof = VOF(i, jj);
if(lvof < vofmin || 1. - vofmin < lvof){
  FLXY(i, j) = vel * lvof;
  continue;
}
double flux = 0.;
for(int ii = 0; ii < NGAUSS; ii++){
  const double w = gauss_ws[ii];
  const double x = gauss_ps[ii];
  flux += w * indicator(NORMAL(i, jj), (const double [NDIMS]){x, y});
}
FLXY(i, j) = vel * flux;

src/interface/update/flxy.c

const double lvof = VOF(i, jj, k);
if(lvof < vofmin || 1. - vofmin < lvof){
  FLXY(i, j, k) = vel * lvof;
  continue;
}
double flux = 0.;
for(int kk = 0; kk < NGAUSS; kk++){
  for(int ii = 0; ii < NGAUSS; ii++){
    const double w = gauss_ws[ii] * gauss_ws[kk];
    const double x = gauss_ps[ii];
    const double z = gauss_ps[kk];
    flux += w * indicator(NORMAL(i, jj, k), (const double [NDIMS]){x, y, z});
  }
}
FLXY(i, j, k) = vel * flux;

src/interface/update/flxz.c

const double lvof = VOF(i, j, kk);
if(lvof < vofmin || 1. - vofmin < lvof){
  FLXZ(i, j, k) = vel * lvof;
  continue;
}
double flux = 0.;
for(int jj = 0; jj < NGAUSS; jj++){
  for(int ii = 0; ii < NGAUSS; ii++){
    const double w = gauss_ws[ii] * gauss_ws[jj];
    const double x = gauss_ps[ii];
    const double y = gauss_ps[jj];
    flux += w * indicator(NORMAL(i, j, kk), (const double [NDIMS]){x, y, z});
  }
}
FLXZ(i, j, k) = vel * flux;

Note

For very small (\(\approx 0\)) or very large (\(\approx 1\)) volume fractions, i.e. single-phase regions,

\[\hat{H} \approx \phi = const.\]

gives a good approximation and thus is directly used.

All the fluxes evaluated at the cell faces are stored in FLXX and FLXY, which are used to update \(\phi\):

src/interface/update/main.c

#if NDIMS == 2
  for(int j = 1; j <= jsize; j++){
    for(int i = 1; i <= isize; i++){
      const double dx = DXF(i  );
      SRC(i, j) += 1. / dx * (
          + FLXX(i  , j  )
          - FLXX(i+1, j  )
      );
    }
  }
#else
  for(int k = 1; k <= ksize; k++){
    for(int j = 1; j <= jsize; j++){
      for(int i = 1; i <= isize; i++){
        const double dx = DXF(i  );
        SRC(i, j, k) += 1. / dx * (
            + FLXX(i  , j  , k  )
            - FLXX(i+1, j  , k  )
        );
      }
    }
  }
#endif

src/interface/update/main.c

#if NDIMS == 2
  for(int j = 1; j <= jsize; j++){
    for(int i = 1; i <= isize; i++){
      SRC(i, j) += 1. / dy * (
          + FLXY(i  , j  )
          - FLXY(i  , j+1)
      );
    }
  }
#else
  for(int k = 1; k <= ksize; k++){
    for(int j = 1; j <= jsize; j++){
      for(int i = 1; i <= isize; i++){
        SRC(i, j, k) += 1. / dy * (
            + FLXY(i  , j  , k  )
            - FLXY(i  , j+1, k  )
        );
      }
    }
  }
#endif

src/interface/update/main.c

for(int k = 1; k <= ksize; k++){
  for(int j = 1; j <= jsize; j++){
    for(int i = 1; i <= isize; i++){
      SRC(i, j, k) += 1. / dz * (
          + FLXZ(i  , j  , k  )
          - FLXZ(i  , j  , k+1)
      );
    }
  }
}

A conventional three-step Runge-Kutta scheme is adopted to integrate the equation in time.

src/interface/update/main.c

    const double coef = rkcoefs[rkstep][rk_a];
    const double * restrict src = interface->src[rk_a].data;
#if NDIMS == 2
    for(int j = 1; j <= jsize; j++){
      for(int i = 1; i <= isize; i++){
        VOF(i, j) += dt * coef * SRC(i, j);
      }
    }
#else
    for(int k = 1; k <= ksize; k++){
      for(int j = 1; j <= jsize; j++){
        for(int i = 1; i <= isize; i++){
          VOF(i, j, k) += dt * coef * SRC(i, j, k);
        }
      }
    }
#endif

src/interface/update/main.c

  if(0 != rkstep){
    const double coef = rkcoefs[rkstep][rk_b];
    const double * restrict src = interface->src[rk_b].data;
#if NDIMS == 2
    for(int j = 1; j <= jsize; j++){
      for(int i = 1; i <= isize; i++){
        VOF(i, j) += dt * coef * SRC(i, j);
      }
    }
#else
    for(int k = 1; k <= ksize; k++){
      for(int j = 1; j <= jsize; j++){
        for(int i = 1; i <= isize; i++){
          VOF(i, j, k) += dt * coef * SRC(i, j, k);
        }
      }
    }
#endif
  }