Third-order methods

Third-order explicit Runge-Kutta methods are given by

\[ \begin{align}\begin{aligned}& q^0 = p^n\\& q^1 = p^n + a_{1,0} f \left( q^0 \right) \Delta t\\& q^2 = p^n + a_{2,0} f \left( q^0 \right) \Delta t + a_{2,1} f \left( q^1 \right) \Delta t\\& q^3 = p^n + a_{3,0} f \left( q^0 \right) \Delta t + a_{3,1} f \left( q^2 \right) \Delta t + a_{3,2} f \left( q^3 \right) \Delta t\\& p^{n + 1} = q^3\end{aligned}\end{align} \]

The Butcher tableau is

\[\begin{split}\begin{array}{c|ccc} b_0 & a_{0,0} & a_{0,1} & a_{0,2} \\ b_1 & a_{1,0} & a_{1,1} & a_{1,2} \\ b_2 & a_{2,0} & a_{2,1} & a_{2,2} \\ \hline & a_{3,0} & a_{3,1} & a_{3,2} \\ \end{array} = \begin{array}{c|ccc} 0 & 0 & 0 & 0 \\ \alpha & \alpha & 0 & 0 \\ \beta & \frac{\beta}{\alpha} \frac{3 \alpha^2 - 3 \alpha + \beta}{3 \alpha - 2} & - \frac{\beta}{\alpha} \frac{\beta - \alpha}{3 \alpha - 2} & 0 \\ \hline & 1 - \frac{3 \alpha + 3 \beta - 2}{6 \alpha \beta} & \frac{3 \beta - 2}{6 \alpha \left( \beta - \alpha \right)} & \frac{- 3 \alpha + 2}{6 \beta \left( \beta - \alpha \right)} \\ \end{array}\end{split}\]

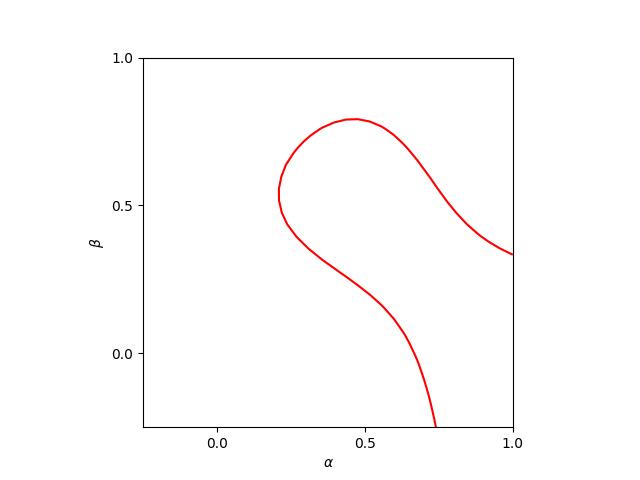
where the elements are constrained by two free parameters \(\left( \alpha, \beta \right)\).

The low-storage schemes can be derived in the same manner as the second-order schemes; namely by substituting \(q^0\) with the previous-step value:

\[ \begin{align}\begin{aligned}& q^0 = p^n\\& r^0 = f \left( q^0 \right)\\& q^1 = q^0 + a_{1,0} r^0 \Delta t\\& r^1 = \frac{a_{2,0} - a_{1,0}}{a_{2,1}} f \left( q^0 \right) + f \left( q^1 \right)\\& q^2 = q^1 + a_{2,1} r^1 \Delta t\\& r^2 = \frac{a_{3,1} - a_{2,1}}{a_{3,2}} \left\{ \frac{a_{3,0} - a_{2,0}}{a_{3,1} - a_{2,1}} f \left( q^0 \right) + f \left( q^1 \right) \right\} + f \left( q^2 \right),\\& q^3 = q^2 + a_{3,2} r^2 \Delta t\\& p^{n + 1} = q^3\end{aligned}\end{align} \]

To be a low-storage scheme, the coefficients need to satisfy

\[\frac{a_{2,0} - a_{1,0}}{a_{2,1}} = \frac{a_{3,0} - a_{2,0}}{a_{3,1} - a_{2,1}},\]

so that \(r^2\) can be directly computed using \(r^1\).

Assigning the Butcher tableau to this relation yields

\[6 \alpha^2 \beta - 6 \alpha \beta^2 + 3 \alpha \beta - 3 \alpha + 6 \beta^2 - 6 \beta + 2 = 0.\]

def find_constraint(a: sympy.Symbol, b: sympy.Symbol) -> sympy.Basic:
    c = 3 * a - 2
    a10 = a
    a20 = b / a * (3 * a * a - 3 * a + b) / c
    a21 = - b / a * (b - a) / c
    a30 = 1 - (3 * a + 3 * b - 2) / (6 * a * b)
    a31 = (3 * b - 2) / (6 * a * (b - a))
    a32 = - c / (6 * b * (b - a))
    eq = (a20 - a10) * (a31 - a21) - a21 * (a30 - a20)
    return sympy.simplify(eq)

The following method is popular among others (Williamson, J. Comput. Phys. (35), 1980).

\[\left( \alpha, \beta \right) = \left( \frac{1}{3}, \frac{3}{4} \right)\]

\[\begin{split}\begin{array}{c|ccc} 0 & 0 & 0 & 0 \\ \frac{1}{3} & \frac{1}{3} & 0 & 0 \\ \frac{3}{4} & \frac{-3}{16} & \frac{15}{16} & 0 \\ \hline & \frac{1}{6} & \frac{3}{10} & \frac{8}{15} \\ \end{array}\end{split}\]

\[\begin{split}\begin{array}{c|ccc} k & 0 & 1 & 2 \\ \hline \beta^k & 0 & \frac{-5}{9} & \frac{-153}{128} \\ \gamma^k & \frac{1}{3} & \frac{15}{16} & \frac{8}{15} \\ \end{array}\end{split}\]