Example

The results of the default case with \(N = 8\) are discussed below. All objects are horizontally aligned (\(\pos_{\ia} = 0\)) with a constant angular velocity:

\[\vel_{\ia} = \sqrt{\frac{6}{2 N + 1}},\]

such that a vertically-aligned and stationary state

\[\pos_{\ia} = \frac{\pi}{2}\]

is one (unstable) solution of the system.

To highlight the effect of the scheme, the energy-conserving scheme and the explicit scheme are compared.

Energy-conserving scheme

cargo run --release

The kinetic energy (\(\kinetic\), red), the potential energy (\(\potential\), blue), and their sum (\(\total\), black) are plotted as a function of time:

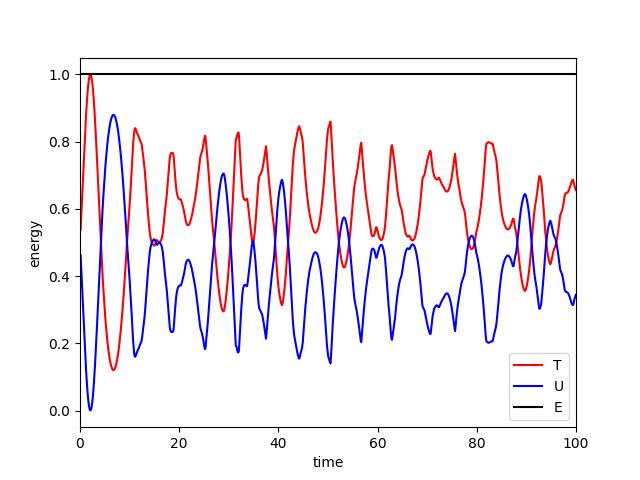
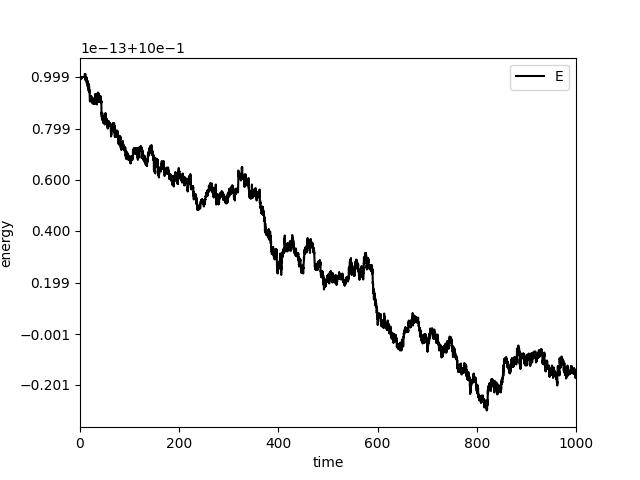
The deviation of the total energy is around the rounding error:

Explicit scheme

cargo run --release --features=explicit

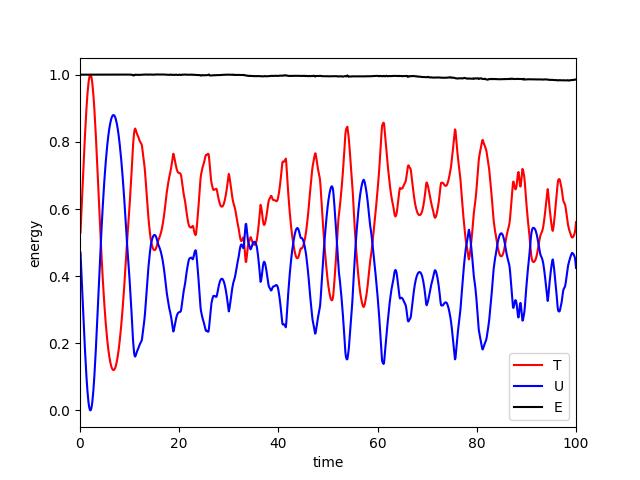
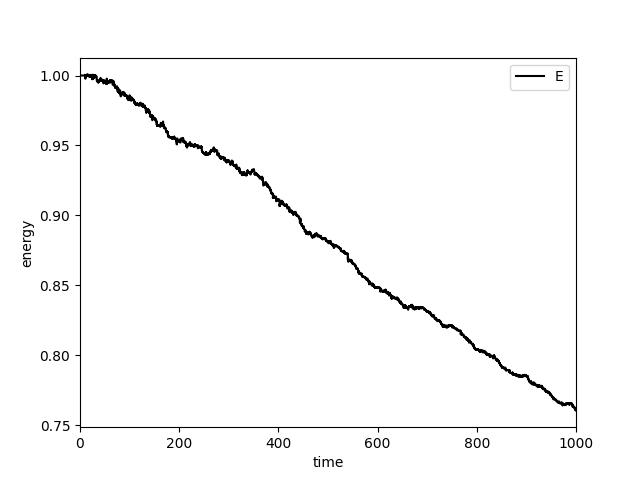
The deviation of the total energy is not around the rounding error:

Although this behavior is improved when the angle is updated using the Crank-Nicolson scheme:

\[\dder{\pos_{\ia}}{t} = \ave{\vel_{\ia}},\]

a clear decreasing trend is still observable. With the Euler explicit scheme:

\[\dder{\pos_{\ia}}{t} = \vel_{\ia}^{n},\]

on the other hand, a clear increasing trend is observed.

In short, as long as a fully-explicit scheme is adopted to update the angular velocity, there is not way to conserve the total energy. Although a simple remedy is of course to make \(\delta t\) smaller, it is impractical to reduce the residual to a rounding error.